一. 题目

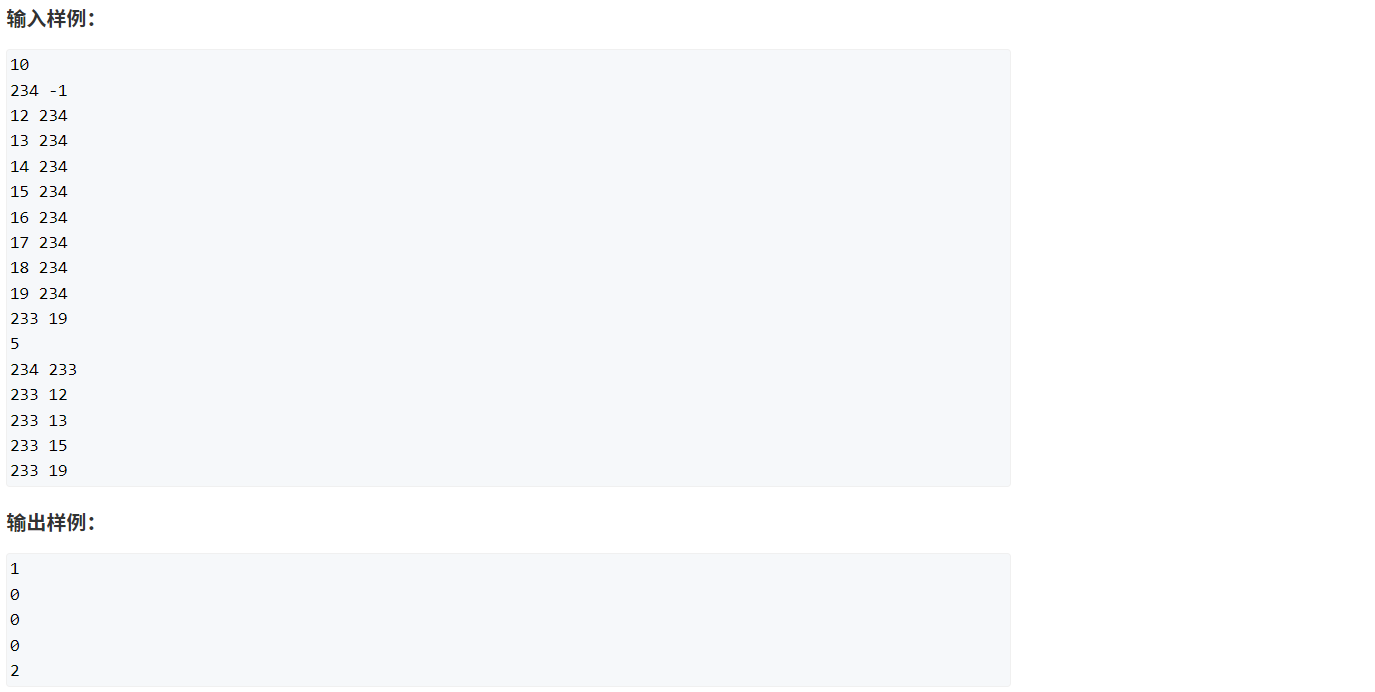
二. 思路

• 倍增法：

• f[i, j]：从节点i开始，向上走2^j次方步所能走到的节点。0<=j<=log(n)。

• depth[i]：表示节点i的深度。

• 首先，将两个点跳到同一层。

• 然后，让两个点同时网上跳，一直到他们最近公共祖先的下一层。

• 预处理O(nlogn)、查询logn。

三. 代码

import java.io.*;
import java.util.*;

public class Main
{
    static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static final BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    static String[] ts;
    static final int N = (int) 4e4 + 10, M = 2 * N, K = 20, INF = Integer.MAX_VALUE;//0~15
    static int[] h = new int[N], e = new int[M], ne = new int[M];
    static int n, m, idx;
    static int[] depth = new int[N];
    static int[][] f = new int[N][K];

    static void add(int a, int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }

    static void dfs(int u, int fa)
    {
        depth[u] = depth[fa] + 1;
        f[u][0] = fa;
        for (int i = 1; i <= 15; ++i)//更新
            f[u][i] = f[f[u][i - 1]][i - 1];

        for (int i = h[u]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (j == fa) continue;
            dfs(j, u);
        }
    }

    static int LCA(int a, int b)
    {
        int t = a;
        if (depth[a] < depth[b])//a的深度大
        {
            a = b;
            b = t;
        }

        for (int i = 15; i >= 0; i--)
            if (depth[f[a][i]] >= depth[b])//若a跳完深度>=b则可以跳
                a = f[a][i];
        if (a == b) return a;

        for (int i = 15; i >= 0; --i)//同一高度
            if (f[a][i] != f[b][i])//a, b跳完不相等
            {
                a = f[a][i];
                b = f[b][i];
            }
        return f[a][0];
    }

    public static void main(String[] args) throws Exception
    {
        Arrays.fill(h, -1);
        ts = br.readLine().split(" ");
        n = Integer.parseInt(ts[0]);

        int root = 0;
        for (int i = 0; i < n; ++i)
        {
            int a, b;
            ts = br.readLine().split(" ");
            a = Integer.parseInt(ts[0]);
            b = Integer.parseInt(ts[1]);
            if (b == -1) root = a;
            else
            {
                add(a, b);
                add(b, a);
            }
        }

        //depth[0] = 0;
        dfs(root, 0);

        ts = br.readLine().split(" ");
        m = Integer.parseInt(ts[0]);
        for (int i = 0; i < m; ++i)
        {
            int a, b;
            ts = br.readLine().split(" ");
            a = Integer.parseInt(ts[0]);
            b = Integer.parseInt(ts[1]);

            int t = LCA(a, b);
            if (t == a) bw.write("1");
            else if (t == b) bw.write("2");
            else bw.write("0");
            bw.newLine();
        }
        bw.close();
    }
}