一. 题目

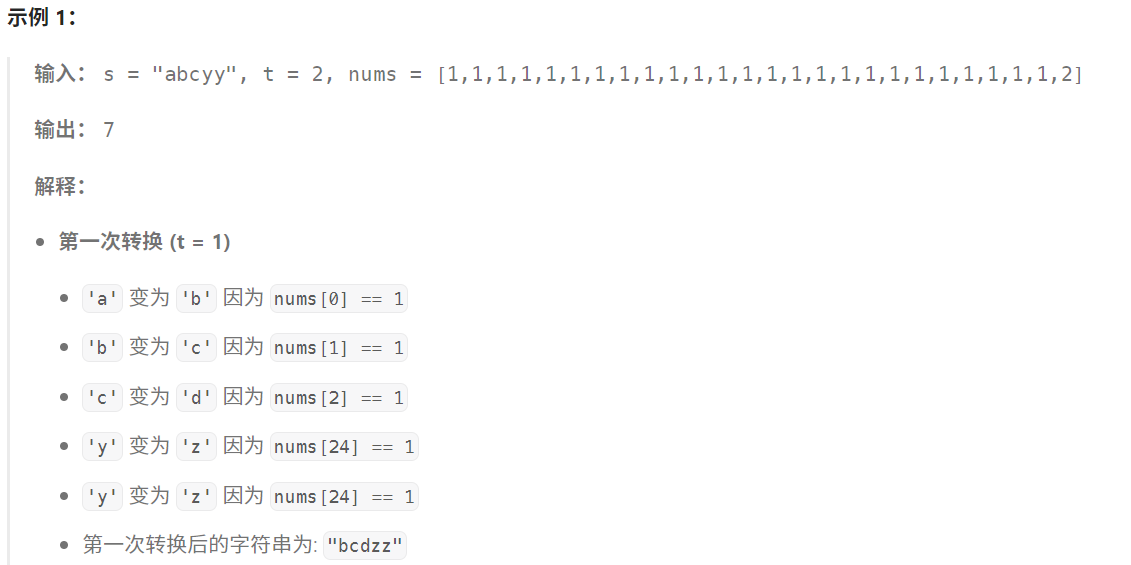
二. 思路

1. DP

• 若t的大小在1s内跑完，可使用此方法。

• f[i,j]：执行i此转换后，字符j的数量。

• f[i+1, nj]+=f[i,j]，i->i+1不用预处理i-1到i时i，j由谁转移了。

2. 矩阵快速幂优化DP

三. 代码

1. DP

class Solution
{
    static final int M = 30, MOD = (int) 1e9 + 7;
    int[][] f = new int[2][M];

    public int lengthAfterTransformations(String s, int t, List<Integer> nums)
    {
        for (Character c : s.toCharArray())
            ++f[0][c - 'a'];

        for (int i = 0; i < t; ++i)
        {
            Arrays.fill(f[i + 1 & 1], 0);//记得清空
            for (int j = 0; j < 26; ++j)
                for (int k = 1; k <= nums.get(j); ++k)
                    f[i + 1 & 1][(j + k) % 26] = (f[i + 1 & 1][(j + k) % 26] + f[i & 1][j]) % MOD;
        }

        int ans = 0;
        for (int i = 0; i < 26; ++i)
            ans = (ans + f[t & 1][i]) % MOD;
        return ans;
    }
}

2. 矩阵快速幂优化DP

class AK
{
    static final int N = 26, MOD = (int) 1e9 + 7;
    int[][] a = new int[N][N];

    static AK getOne()//得到单位矩阵
    {
        AK o = new AK();
        for (int i = 0; i < N; ++i)
            o.a[i][i] = 1;
        return o;
    }

    AK mul(AK o)//自身X另一个矩阵
    {
        AK res = new AK();
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                for (int k = 0; k < N; ++k)
                    res.a[i][j] = (int) ((res.a[i][j] + (long) a[i][k] * o.a[k][j]) % MOD);
        return res;
    }

    static AK qmi(AK a, int k)//快速幂
    {
        AK ans = getOne();
        while (k > 0)
        {
            if ((k & 1) == 1) ans = ans.mul(a);
            a = a.mul(a);
            k >>= 1;
        }
        return ans;
    }
}

class Solution
{
    int[] f = new int[AK.N];

    public int lengthAfterTransformations(String s, int t, List<Integer> nums)
    {
        for (Character c : s.toCharArray())//得到f[0]
            ++f[c - 'a'];
        AK T = new AK();
        for (int i = 0; i < AK.N; ++i)//得到初始T
            for (int j = 1; j <= nums.get(i); ++j)
                T.a[(i + j) % 26][i] = 1;

        AK res = AK.qmi(T, t);//得到快速幂后的T
        int ans = 0;
        for (int i = 0; i < AK.N; ++i)//最后一次乘
            for (int j = 0; j < AK.N; ++j)
                ans = (int) ((ans + (long) res.a[i][j] * f[j]) % AK.MOD);
        return ans;
    }
}