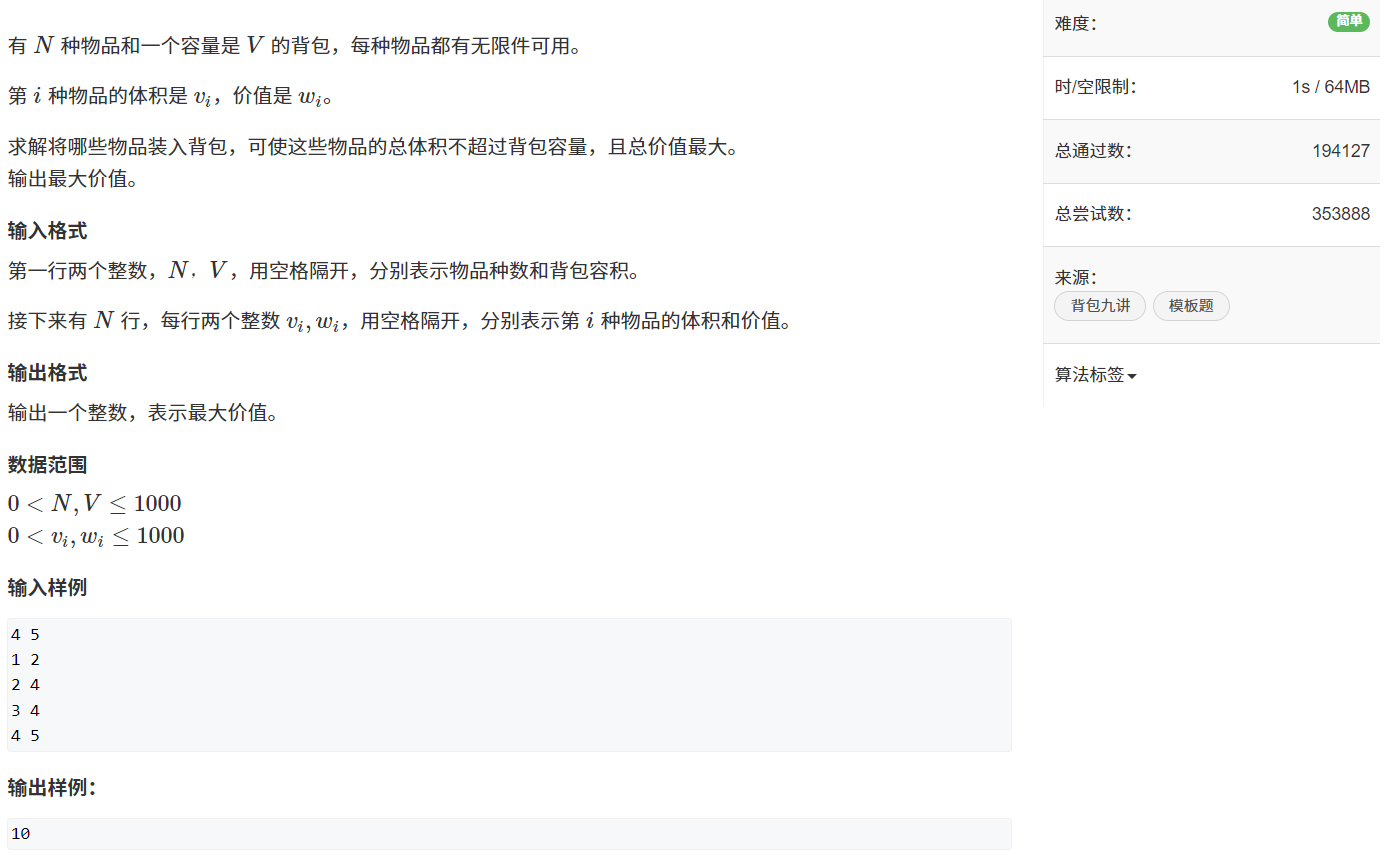
一. 题目

二. 思路

• f[i][j-v]已经表示了从前i个选，体积为j-v时的最优情况(最优子结构)，所以当前再选至多再选一次，体积为j。

三. 代码

1. 朴素

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e3+10;

int n, m;
int v[N], w[N];
int f[3][N];

signed main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        scanf("%d%d", &v[i], &w[i]);
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            for(int k=0;k*v[i]<=j;k++)//枚举第i个物品选几个, 选0个就是不选
                f[i&1][j]=max(f[i&1][j], f[i-1&1][j-k*v[i]]+k*w[i]);
    cout<<f[n&1][m]<<endl;
}

2. 优化二维

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <queue>
using namespace std;
const int N=1e3+10;

int n, m;
int v[N], w[N];

class DP
{
public:
    int f[2][N];
    //由于只用到i层和i-1层，所以可以只存两层内容

public:
    DP()
    {
        initIO();
        fill(f[0], f[0]+2*N, 0);
    }

    void initIO()
    {
        ios::sync_with_stdio(false);
        cin.tie(nullptr), cout.tie(nullptr);
    }

    int work()
    {
        for(int i=1;i<=n;++i)
            for(int j=0;j<=m;++j)
            {
                f[i&1][j]=f[i-1&1][j];
                if(j>=v[i])
                    f[i&1][j]=max(f[i&1][j], f[i&1][j-v[i]]+w[i]);
            }

        return f[n&1][m];
    }
}dp;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;++i)
        cin>>v[i]>>w[i];
    cout<<dp.work();
}