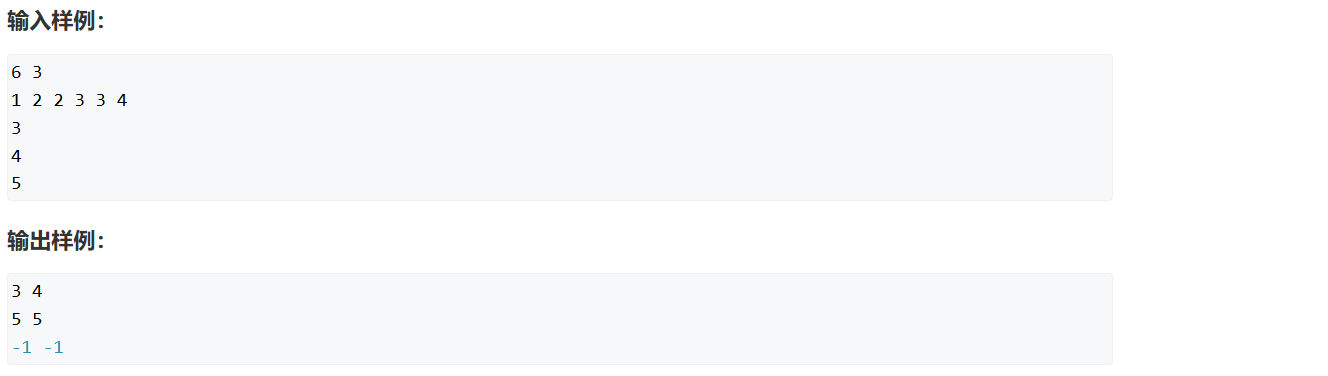
一. AcWing789_数的范围

二. 理论

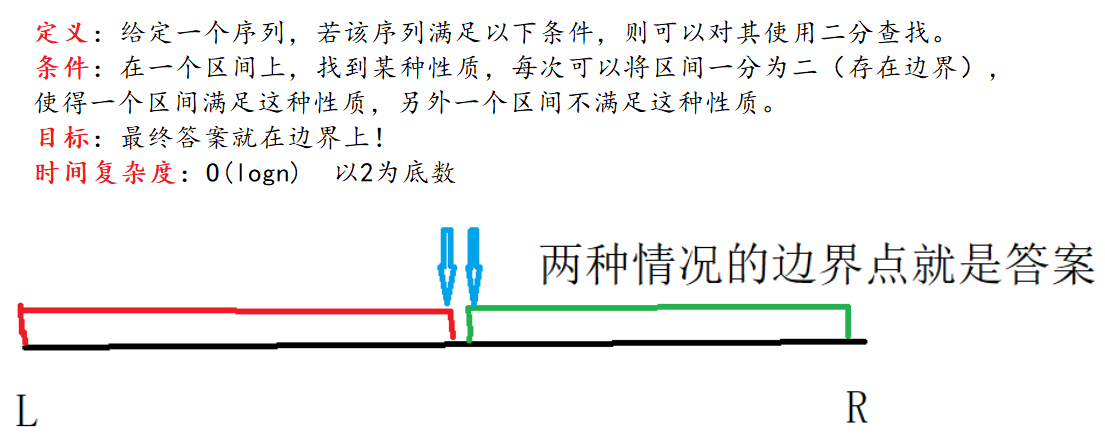
• 对于本题给定一个升序序列，查找元素k的起始位置和终止位置，只需分别使用二分查找起始位置和终止位置即可。

• 对于起始位置，即查找最左边的元素k的位置，二分的更新则使用mid=r，不断靠近左边

三. 代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e5+10;

int n, m, k;
int q[N];

//朴素二分类
class Dichotomy
{
public:
    static void initIO()
    {
        // 关闭输入输出缓存，使效率提升
        ios::sync_with_stdio(false);
        // 解除cin和cout的默认绑定，来降低IO的负担使效率提升
        cin.tie(nullptr);
        cout.tie(nullptr);
    }

    /**
     * 查找左边界
     * @param l 区间左值
     * @param r 区间右值
     * @param x 要查找的值
     * @return 返回左边界下标，没有则返回-1。
     */
    int findl(int l, int r, int x)
    {
        while(l<r)
        {
            int mid=(l+r)/2;
            if(q[mid]>=x) r=mid;
            else l=mid+1;
        }

        return l;
    }

    /**
     * 查找右边界
     * @param l 区间左值
     * @param r 区间右值
     * @param x 要查找的值
     * @return 返回右边界下标，没有则返回-1。
     */
    int findr(int l, int r, int x)
    {
        while(l<r)
        {
            int mid=(l+r+1)/2;
            if(q[mid]<=x) l=mid;
            else r=mid-1;//出现mid-1，则上面(l+r+1)而不是(l+r)防止死循环
        }

        return l;
    }
};

int main()
{
    Dichotomy::initIO();
    
    cin>>n>>m;
    for(int i=0;i<n;++i)
        cin>>q[i];
    
    Dichotomy dichotomy;
    while(m--)
    {
        cin>>k;
        int idx=dichotomy.findl(0, n-1, k);
        if(q[idx]!=k) cout<<"-1 -1"<<endl;
        else cout<<idx<<" "<<dichotomy.findr(0, n-1, k)<<endl;
    }
}