一. 题目

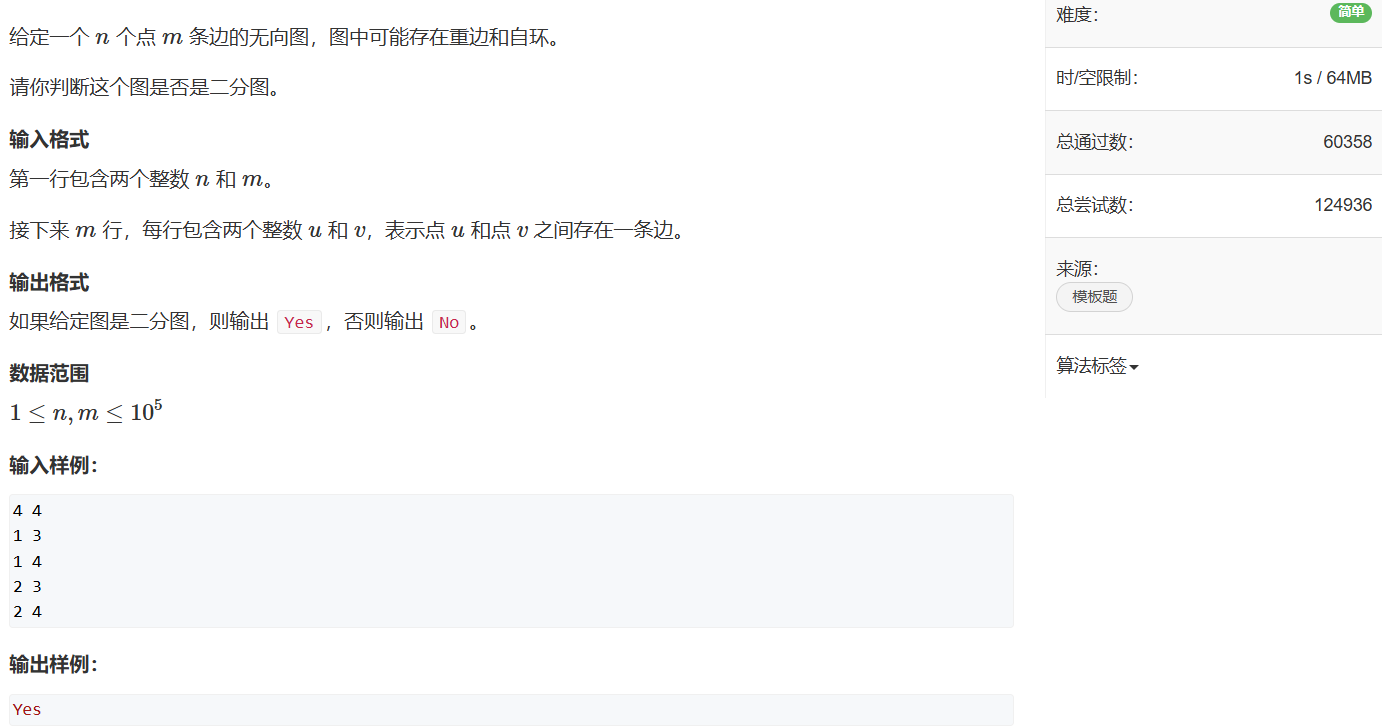
二. 思路

• 二分图：二分图（Bipartite Graph）是一种特殊的图，其顶点可以分为两个不相交的集合，且图中的每条边都连接这两个集合中的顶点。

• 可二分性：如果一个图是二分图，则它是可以用两种颜色来涂色的，使得相邻的顶点颜色不同。

• 无奇环：二分图不包含长度为奇数的环。

• 思路：利用dfs进行染色，最后若产生矛盾(同色)则返回false, 若返回true代表为二分图。

• 时间复杂度：O(n+m)

三. 代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N=1e5+10, M=2*N;

int n, m;

class SingleLinkedList
{
public:
    int h[N], e[M], ne[M], idx;
public:
    SingleLinkedList()
    {
        initIO(), idx=0;
        fill(h, h+N, -1);
        fill(e, e+M, 0);
        fill(ne, ne+M, 0);
    }

    void initIO()
    {
        ios::sync_with_stdio(false);
        cin.tie(nullptr), cout.tie(nullptr);
    }

    void add(int a, int b)
    {
        e[idx]=b, ne[idx]=h[a], h[a]=idx++;
    }
}sll;

class BipartiteGraph
{
public:
    int color[N];
public:
    BipartiteGraph()
    {
        fill(color, color+N, -1);//初始无颜色为-1
    }

    bool dfs(int u, int c)//走到哪个节点，以及当前节点染成什么色
    {
        color[u]=c;
        for(int i=sll.h[u];~i;i=sll.ne[i])
        {
            int j=sll.e[i];
            if(color[j]==c) return false;//子节点和当前节点冲突
            if(color[j]==-1&&!dfs(j, !c)) return false;//子节点里有冲突
        }
        return true;//若都无冲突
    }
}bg;

int main()
{
    cin>>n>>m;
    while(m--)
    {
        int a, b;
        cin>>a>>b;
        sll.add(a, b);
        sll.add(b, a);
    }
    
    bool isBG=true;
    for(int i=1;i<=n;++i)
        if(bg.color[i]==-1&&(!bg.dfs(i, 0)))
        {
            isBG=false;
            break;
        }
    if(isBG) cout<<"Yes";
    else cout<<"No";
}