一. 题目

二. 理论

• 

• 

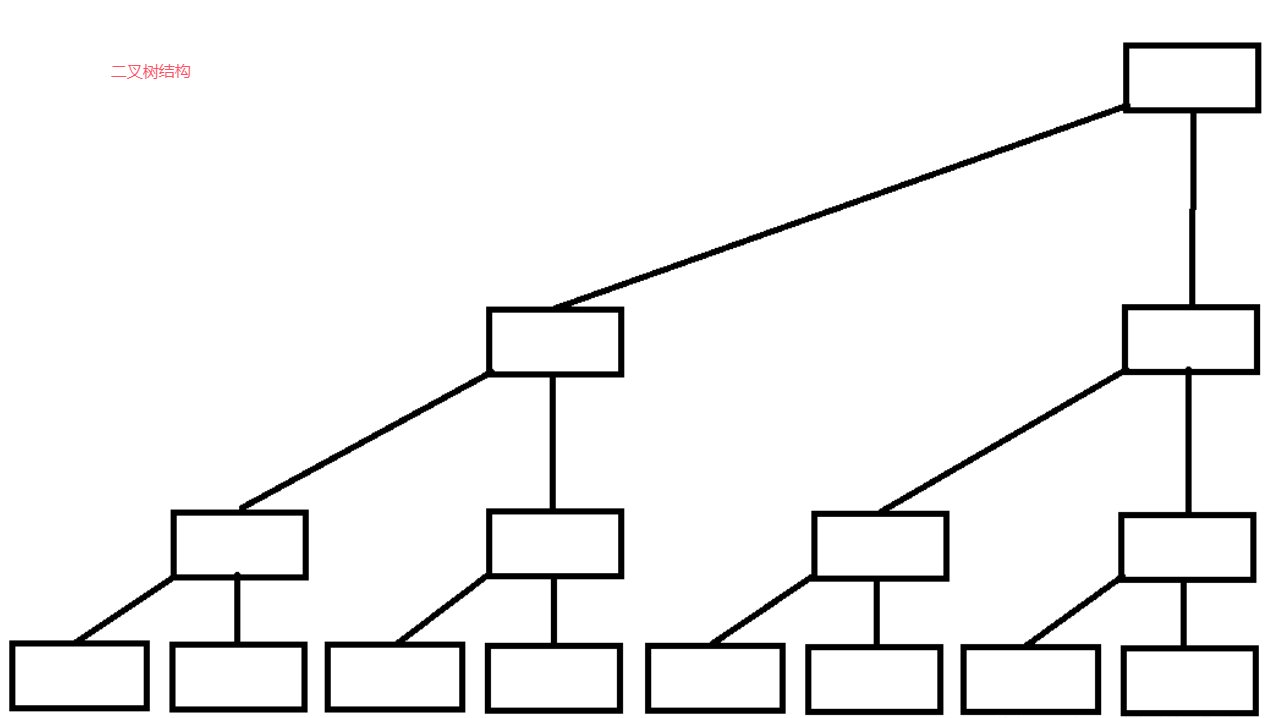
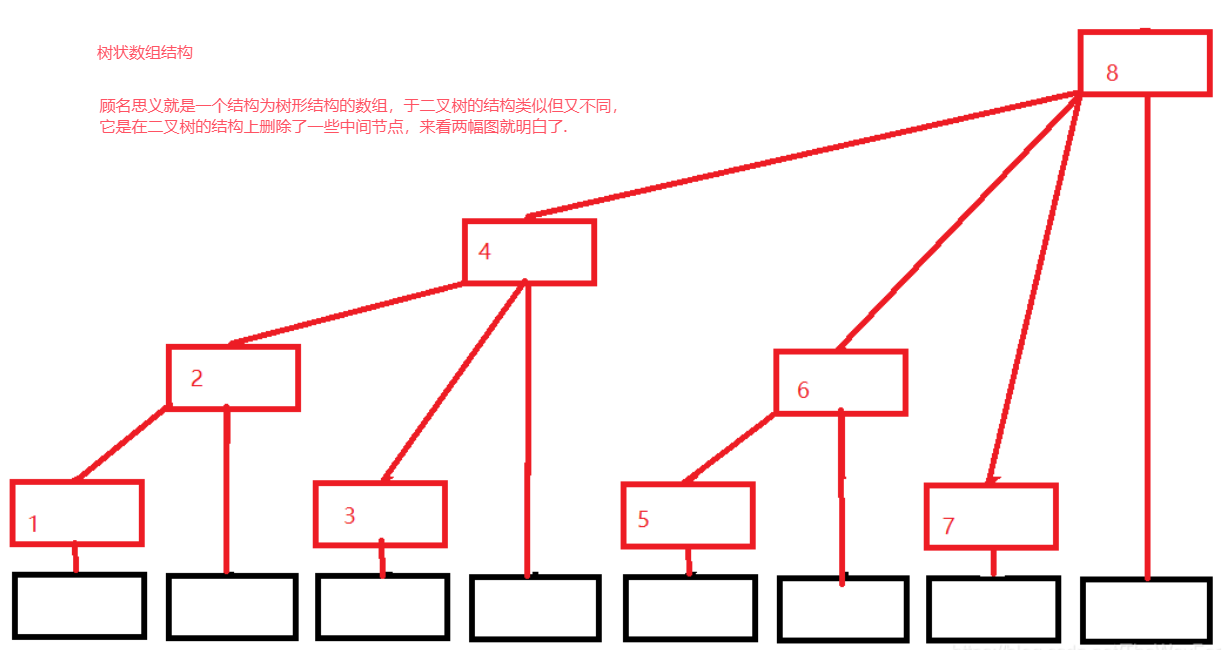
• 树状数组结构分析

• 

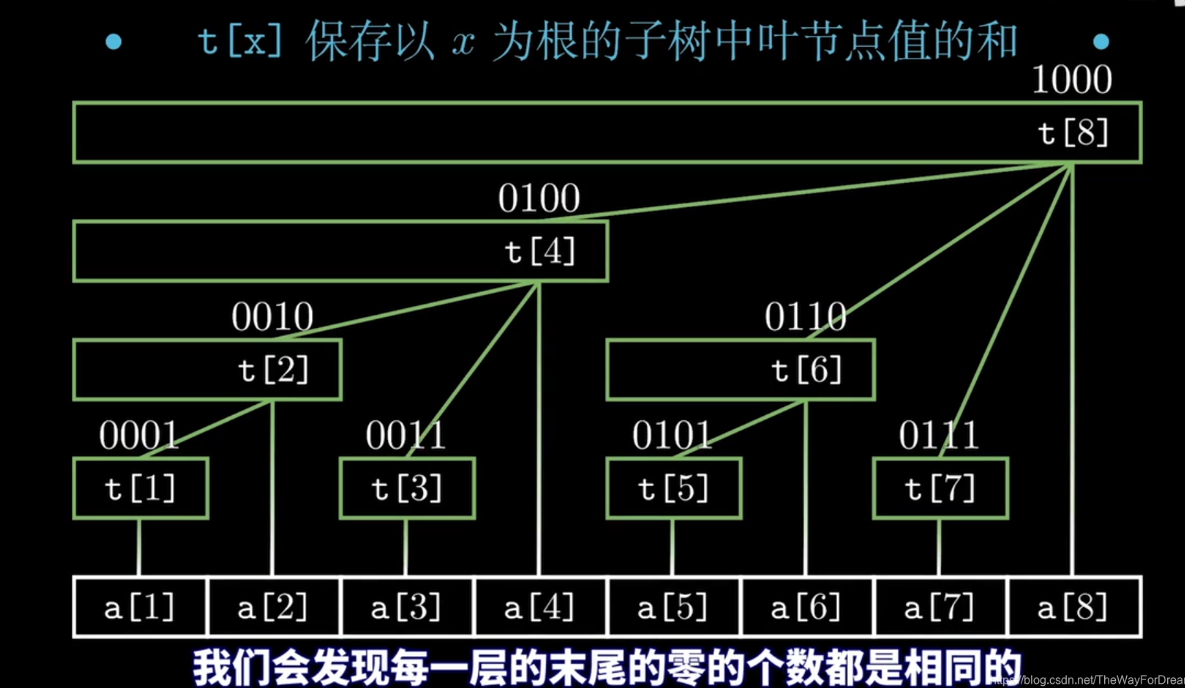
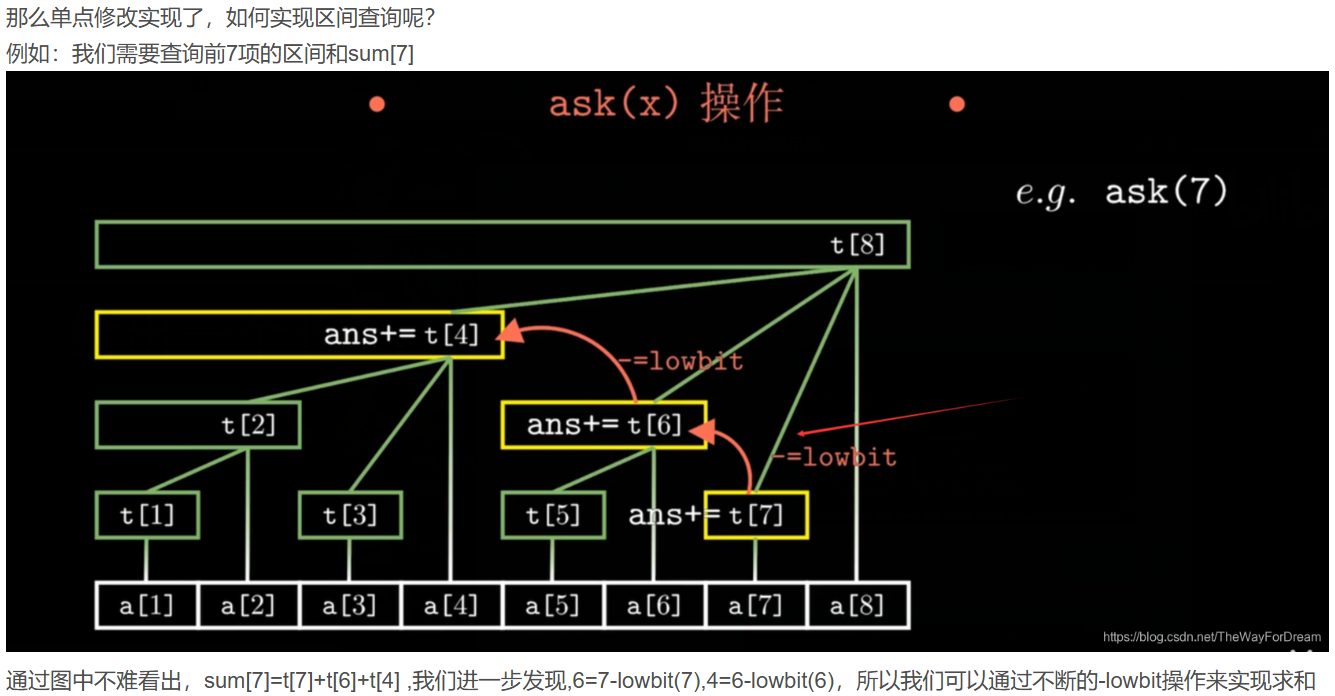
• 上面时树状数组的结构图，t[x]保存以x为根的子数中叶子节点值的和,原数组为a[]那么原数组前4项的和t[4]=t[2]+t[3]+a[4]=t[1]+a[2]+t[3]+a[4]=a[1]+a[2]+a[3]+a[4],看似没有什么特点，别着急往下看

• 

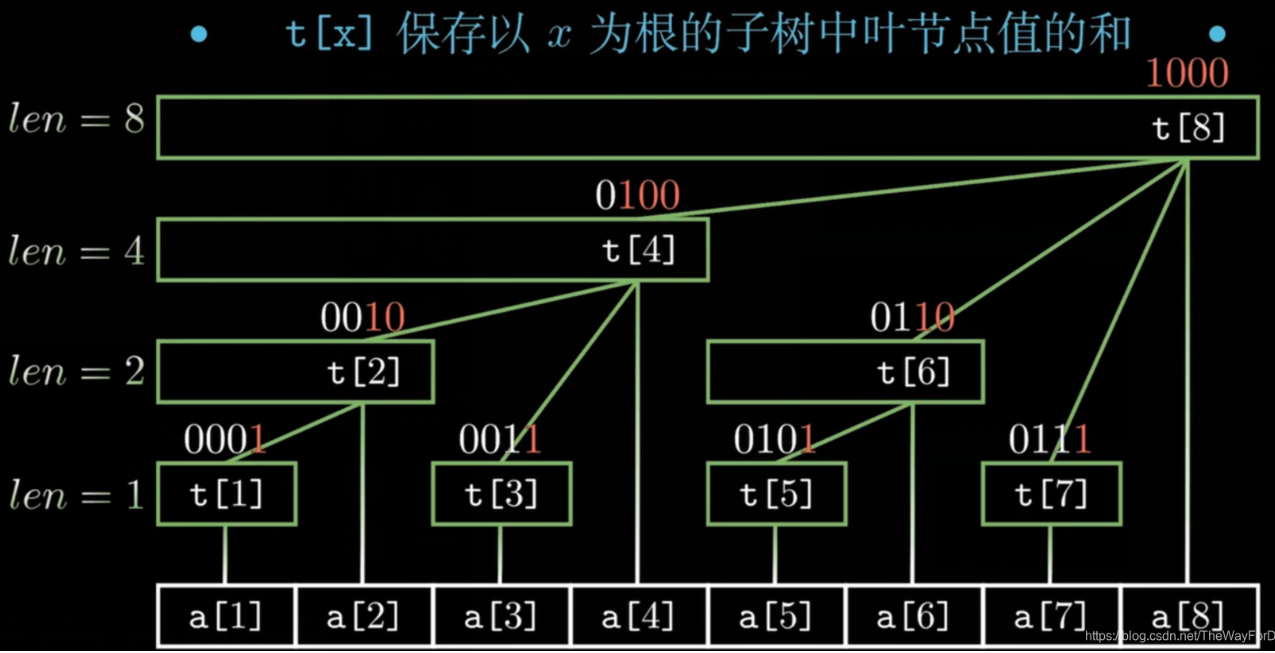
• 我们通过观察节点的二进制数，进一步发现，树状数组中节点x的父节点为x+lowbit(x),例如t[2]的父节点为t[4]=t[2+lowbit(2)]

• 

• 

• 

• 本题思路：

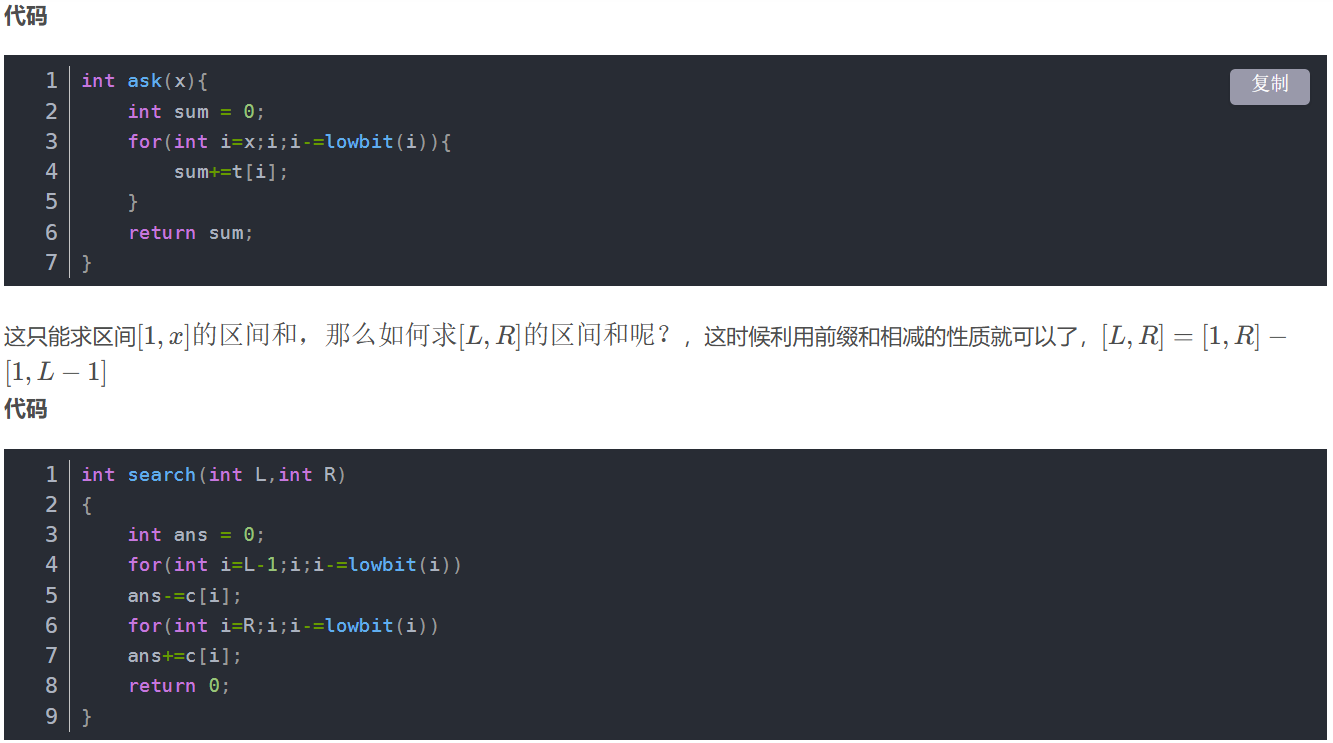
• 从左往右遍历，y值作为下标，在其下标处加1，表示这个值出现过，利用树状数组统计下对于第i个数左边有多少比他小的，比他大的。左边比i小的就是getSum(a[i]-1)，左边比他大的就是当前总数减<=a[i]的，getSum(n)-getSum(a[i])

• 从右往左遍历，右边有多少比他小的，比他大的即可。右边比他小的就是getSum(a[i]-1), 右边比他大的是getSum(n)-getSum(a[i])

• 最后组合数学，相乘统计即可

三. 代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
const int N=2e5+10;
using LL=long long;

int n;
int a[N];

class TreeArray
{
public:
    int tr[N];
public:
    TreeArray()
    {
        initIO();
        init();
    }

    void init()
    {
        fill(tr, tr+N, 0);
    }

    void initIO()
    {
        ios::sync_with_stdio(false);
        cin.tie(nullptr), cout.tie(nullptr);
    }

    //返回x的最后一位1
    int lowbit(int x)
    {
        return x&-x;
    }

    void add(int x, int v)
    {
        for(int i=x;i<=n;i+=lowbit(i))
            tr[i]+=v;
    }

    //得到从1~x这段的和
    int getSum(int x)
    {
        int sum=0;
        for(int i=x;i;i-= lowbit(i))
            sum+=tr[i];
        return sum;
    }

    //得到区间和，利用前缀和思想
    int getLRV(int l, int r)
    {
        return getSum(r)-getSum(l-1);
    }
}ta;

class Info
{
public:
    int lmin, lmax;//左边比当前小的大的数量
    int rmin, rmax;//右边比当前小的大的数量
public:
    Info()
    {
        lmin=lmax=rmin=rmax=0;
    }
}info[N];

int main()
{
    cin>>n;
    for(int i=1;i<=n;++i)
    {
        cin>>a[i], ta.add(a[i], 1);
        info[i].lmin=ta.getSum(a[i]-1);
        info[i].lmax=ta.getLRV(a[i]+1, n);
    }

    ta.init();
    for(int i=n;i;--i)
    {
        ta.add(a[i], 1);
        info[i].rmin=ta.getSum(a[i]-1);
        info[i].rmax=ta.getLRV(a[i]+1, n);
    }

    LL ansA=0, ansT=0;
    for(int i=1;i<=n;++i)
    {
        ansA+=1ll*info[i].lmax*info[i].rmax;
        ansT+=1ll*info[i].lmin*info[i].rmin;
    }
    cout<<ansA<<" "<<ansT;
}