一. AcWing831_KMP字符串

二. 理论

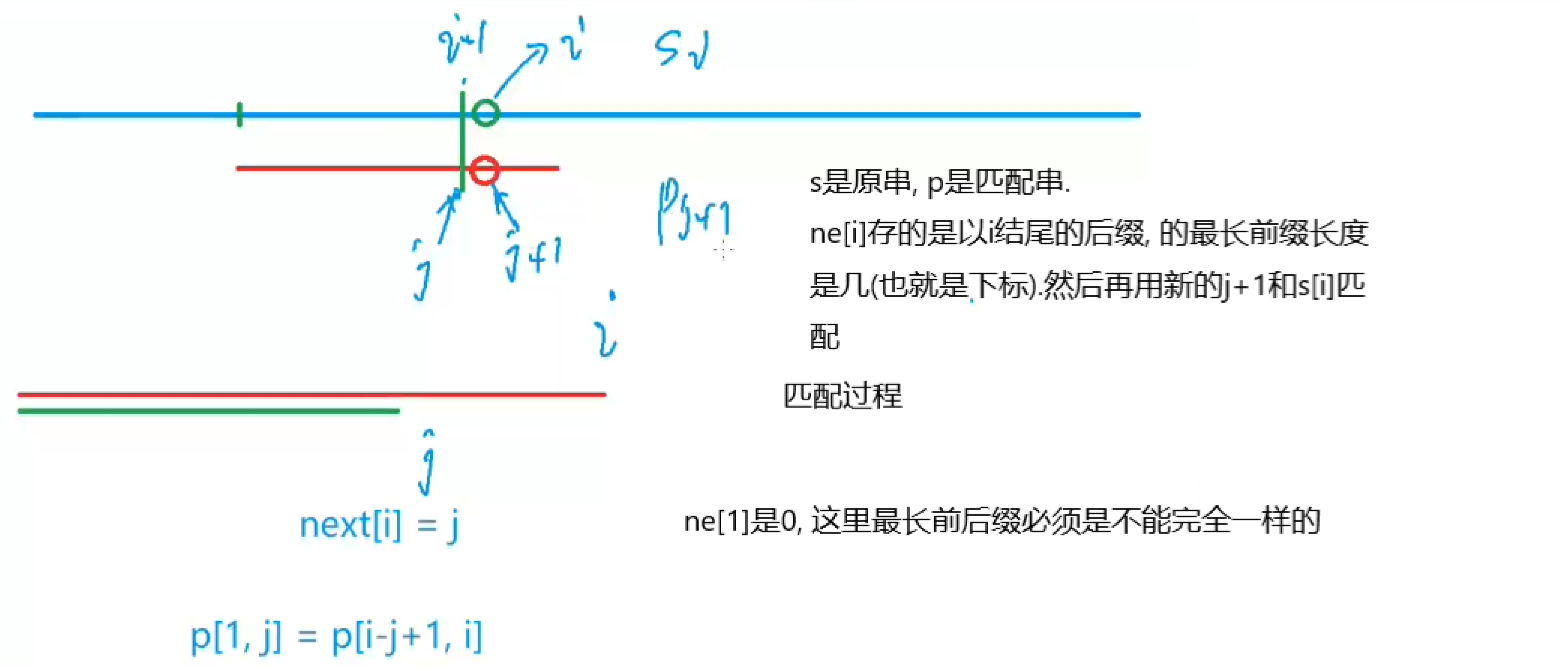
1. kmp原理

2. 循环节

• KMP算法中最重要的就是next数组，next[i]表示是字符串中所有以 i 为结尾的非前缀子串中与前缀能匹配的长度的最大值。可能有点绕，缕一缕吧，这就是next[ ]数组的定义而已。

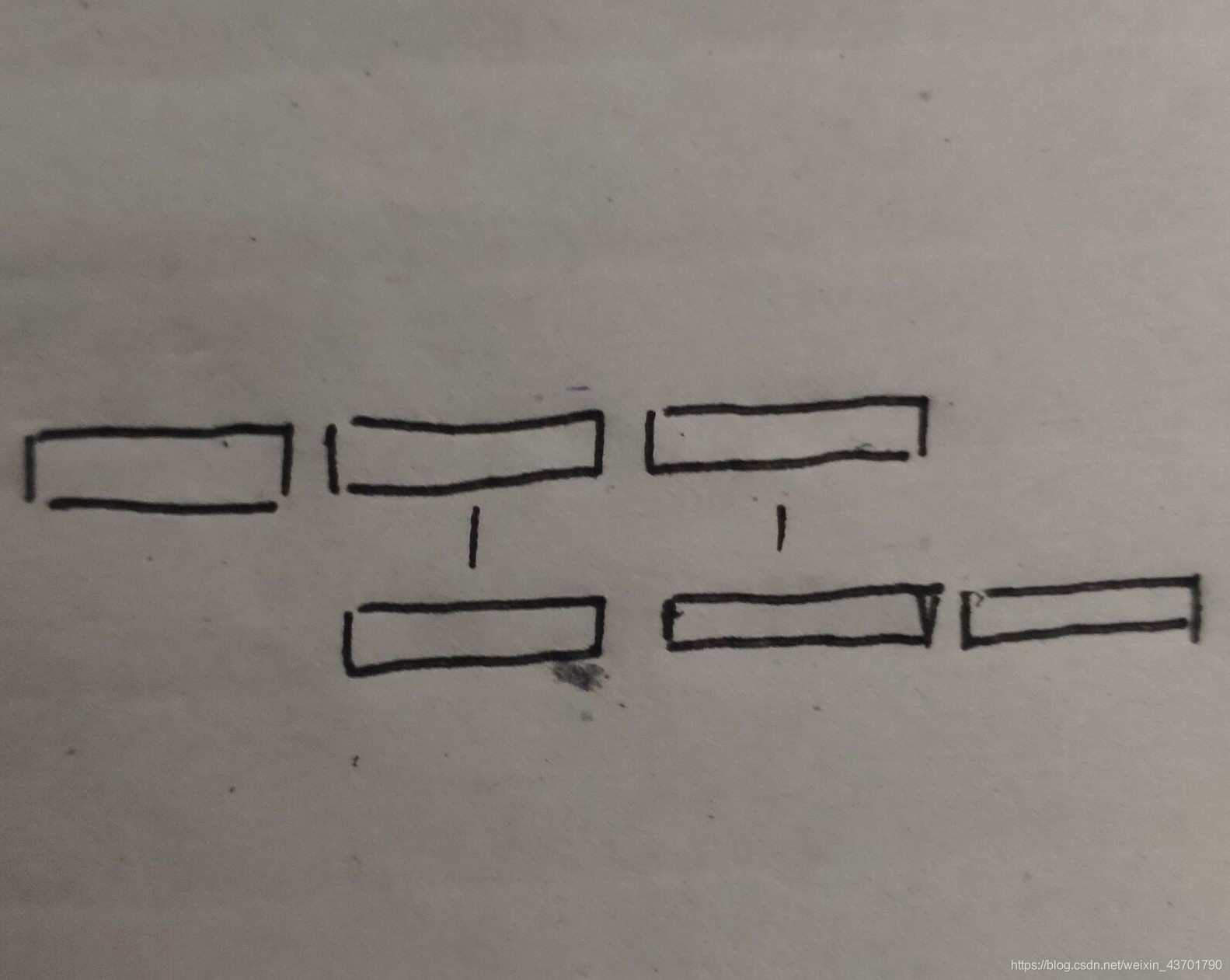
• 我们求最小循环节也是利用next[ ]数组求的。假设字符串是一个循环字符串，可以有一个循环节循环多次得到(假设多于一次)，不妨假设循环节是str1，原来的字符串肯定是由循环节循环而来，即string=str1str1...str1，如果字符串长度为len，根据next[ ]数组的定义，next[len]就是以字符串结尾为结尾的非前缀与前缀匹配的最大长度，如果这个字符串能由一个循环节循环多次得到，那么next[n]中一定包含了至少一次循环节，而且是去掉了从头开始的第一个循环节后的整个字符串。自己在本子上画一下就好了。对齐方式肯定是下图这个样子，每一个方框都是一个循环节。

• 因为我们设的是最小循环节，如果认为有其他方法，那么一定可以将第二个字符串对齐的时候向前移动，如果这样的话那么它肯定不是最小循环节。既然这样，最小循环节长度就是len - next[len]，如果能由它循环多次得来，一定满足满足以下条件。

• len % (len - next[len]) == 0

• 如果len - next[len] == len 说明整个字符串是一个循环节，特判一下就好了。当然这个求的最小循环节，次小的循环节应该是len - next[next[len]]，以此类推，当然需要判断一下啦。

• 若该字符串不是完全由循环节组成，则需要补充的字母数使其成为完全由循环节组成：L-len%L(L是最小循环节长度)

三. 代码

#include<iostream>
#include<cstdio>
using namespace std;
namespace Question
{
    const int N=1e5+10, M=1e6+10;
    int n, m;
    char s[M];//匹配串
}
using namespace Question;

namespace KMP
{
    char p[N];//模式串 
    int ne[N];//每个位置最长非平凡前缀是多少
    
    void init()//预处理ne数组
    {
        //ne[0]=ne[1]=0, 0是起点
        for(int i=2, j=0;i<=n;i++)//处理ne数组
        {
            while(j&&p[i]!=p[j+1]) j=ne[j];
            if(p[i]==p[j+1]) j++;
            ne[i]=j;
        }
    }
}
using namespace KMP;

signed main()
{
    cin>>n>>p+1>>m>>s+1;
    
    init();
    for(int i=1, j=0;i<=m;i++)//匹配
    {
        while(j&&s[i]!=p[j+1]) j=ne[j];//当s[i]!=p[j+1]且j没有退回起点(0)时, 就一直往前跳
        if(s[i]==p[j+1]) j++;//若匹配成功, j向后移动一位
        if(j==n)//完全匹配
        {
            j=ne[j];//在跳一次, 找下一个,若这里j=0, 表示不能重复
            printf("%d ", i-n);//找到在s中的起点, 下标从0开始所以i-n
        }
    }
}